-
UID:317649
-
- 注冊(cè)時(shí)間2020-06-19
- 最后登錄2025-10-22
- 在線時(shí)間1881小時(shí)
-
-
訪問TA的空間加好友用道具

|
在系統(tǒng)的不同平面上,電磁場分量的傅里葉變換是連接空間域和k域的物理光學(xué)建模中的頻繁操作。我們介紹一個(gè)場所謂的幾何區(qū)域,在該區(qū)域中傅里葉變換可以在不進(jìn)行積分的情況下得到,總之是以非常有效的數(shù)值方式得到。在幾何場域中,場由波前相位控制,因此允許我們將穩(wěn)定相位的概念應(yīng)用于傅里葉變換積分,我們將所得到的傅里葉變換算法稱為幾何傅立葉變換,這項(xiàng)技術(shù)被證明是快速物理光學(xué)的基礎(chǔ)支柱。 �&"DD&87N%
�%lGT�|XrY 1.光學(xué)傅立葉變換 *0Wk�z�'=U
$ZlzS`XF�7 在物理光學(xué)中,我們處理電磁場的六個(gè)復(fù)數(shù)場分量(分別為E和H)。在空間域,他們表示為 s:oj��lmPb
jJAr� #�|�
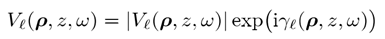 y�=zs6�HaS <SiJA`(7� 其中 y�=zs6�HaS <SiJA`(7� 其中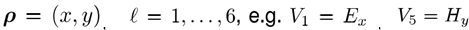 ,傅立葉變換到k域定義為 �2��]V��8- ,傅立葉變換到k域定義為 �2��]V��8- 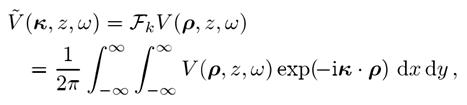 (2) 3j�2�d&�*0 其中,我們使用符號(hào) >N"=1����0 (2) 3j�2�d&�*0 其中,我們使用符號(hào) >N"=1����0
(5��kL6d2�
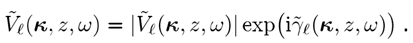 (3) ���q+ka}@ \�m(>�Q��� 方程2中積分的數(shù)值評(píng)估需要對(duì)a和k域中的場進(jìn)行取樣,我們用N表示采樣點(diǎn)的數(shù)量,所得的離散傅里葉變換構(gòu)成了N2運(yùn)算。然而快速傅里葉變換(FFT)算法在N中是線性的,這在原理上使快速物理光學(xué)建模成為可能,但FFT需要 (3) ���q+ka}@ \�m(>�Q��� 方程2中積分的數(shù)值評(píng)估需要對(duì)a和k域中的場進(jìn)行取樣,我們用N表示采樣點(diǎn)的數(shù)量,所得的離散傅里葉變換構(gòu)成了N2運(yùn)算。然而快速傅里葉變換(FFT)算法在N中是線性的,這在原理上使快速物理光學(xué)建模成為可能,但FFT需要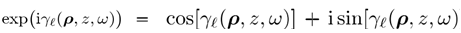 的采樣。在光學(xué)中,我們通常有強(qiáng)梯度的相位函數(shù),從而導(dǎo)致很大的N值,只有在十分對(duì)稱的光學(xué)系統(tǒng)中,N才可以很小。因此,盡管FFT在N中是線性的,但是我們很容易在光學(xué)上遇到N太大而不能進(jìn)行快速計(jì)算傅里葉變換的問題,這是快速物理光學(xué)概念的嚴(yán)重阻礙。 �r{�wf;5d( 的采樣。在光學(xué)中,我們通常有強(qiáng)梯度的相位函數(shù),從而導(dǎo)致很大的N值,只有在十分對(duì)稱的光學(xué)系統(tǒng)中,N才可以很小。因此,盡管FFT在N中是線性的,但是我們很容易在光學(xué)上遇到N太大而不能進(jìn)行快速計(jì)算傅里葉變換的問題,這是快速物理光學(xué)概念的嚴(yán)重阻礙。 �r{�wf;5d(
�����FpZ5@ 為了進(jìn)一步研究,我們用波前相位Ψ將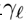 分解(跳過ω)為 vdd>\r)v�� 分解(跳過ω)為 vdd>\r)v��
K~+x��@O�*
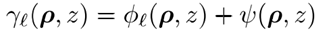 (4) ! q+>'M��t 74�a� k|(! 對(duì)于所有分量都是一樣的。 顯然,方程 4中的分解是模糊的,其依賴于從源場出發(fā)建模中恰當(dāng)?shù)南辔惶幚矸绞健S啥x (4) ! q+>'M��t 74�a� k|(! 對(duì)于所有分量都是一樣的。 顯然,方程 4中的分解是模糊的,其依賴于從源場出發(fā)建模中恰當(dāng)?shù)南辔惶幚矸绞健S啥x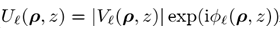 得分解結(jié)果 7%W@Hr,%�F 得分解結(jié)果 7%W@Hr,%�F
2
|