本文介紹了模擬光在均勻介質(zhì)中傳播的四種快速而嚴(yán)格的方法。結(jié)果表明，在自由空間傳播中，對(duì)光滑強(qiáng)相位項(xiàng)的解析處理在減少計(jì)算量方面是非常有效的。因此，在不限制快速傅里葉變換算法應(yīng)用的情況下，我們重新設(shè)計(jì)了平面波角譜（SPW）算子來處理線性、球形和一般光滑相位項(xiàng)。特別是對(duì)于非傍軸場(chǎng)傳播，所提出的技術(shù)可以顯著地減少所需的采樣點(diǎn)數(shù)量。數(shù)值結(jié)果表明了新方法的有效性和準(zhǔn)確性。 LU9A#  
3JVK  
一.文章介紹 El@(mOu|  
="g*\s?r  
光學(xué)建模與設(shè)計(jì)是研究與開發(fā)中極其重要的一部分。由于人們對(duì)高質(zhì)量光學(xué)系統(tǒng)（包括衍射光學(xué)和微光學(xué)、散射物體和部分相干源）的需求日益增加，基于幾何光學(xué)和物理光學(xué)相結(jié)合的模擬方法，即場(chǎng)追跡變得非常重要。這種模擬技術(shù)的一個(gè)重要部分是諧波場(chǎng)在均勻介質(zhì)中的傳播。然而，能夠快速、準(zhǔn)確地模擬一般光場(chǎng)在自由空間中的傳播仍然是一項(xiàng)具有挑戰(zhàn)性的任務(wù)。常用的算法只能做到快速或者只是準(zhǔn)確。 [3@):8  
l~M_S<4n  
在本文中，我們沒有進(jìn)一步的物理近似，介紹了四種新的算法，基于平面波（SPW）算子的角譜，有效地計(jì)算包含平滑但強(qiáng)相位項(xiàng)的非傍軸矢量光場(chǎng)的傳播。根據(jù)光滑相位項(xiàng)的形狀，可以使用不同的傳播算子。它們的共同點(diǎn)是避免了光滑相位項(xiàng)指數(shù)函數(shù)的采樣。相反，平滑相位項(xiàng)是解析處理的，只需對(duì)殘差進(jìn)行采樣即可執(zhí)行傳播操作；因此，稱為半解析傳播技術(shù)。 yUp,NfS]o  
OD5m9XS  
首先，在第二節(jié)中我們給出一個(gè)問題的描述并引入數(shù)學(xué)符號(hào)。然后，在第3節(jié)中，我們考慮了一個(gè)球面相位項(xiàng)，Mansuripur[6]為此引入了一種嚴(yán)格的技術(shù)，稱為使用快速傅里葉變換（FFT）的擴(kuò)展菲涅耳衍射積分。在本節(jié)中，通過應(yīng)用Van der Avoort等人最初使用的數(shù)值合適的拋物線擬合技術(shù)改進(jìn)了該概念。在另一種情況下[7]，詳細(xì)討論了擴(kuò)展菲涅耳算子在數(shù)值上可行的參數(shù)空間。此外，我們還介紹了擴(kuò)展的菲涅耳算符的快速反演方法，用于快速計(jì)算非傍軸場(chǎng)到焦點(diǎn)區(qū)域的傳播。 L>YU,I\o  
     3Oi nK['  
在第四節(jié)中，我們描述了一個(gè)用于光場(chǎng)快速傳播的半解析SPW算子，它包含一個(gè)光滑的線性相位項(xiàng)。該方法基于線性相位項(xiàng)和橫向偏移量的解析處理。之后，我們將這兩種技術(shù)結(jié)合起來，得到了一個(gè)數(shù)值有效的半解析SPW算子，它能夠同時(shí)解析地處理線性和球形相位項(xiàng)。 h}xeChw]  
   m o:D9  
最后，在第6節(jié)中，我們通過將光場(chǎng)分解成具有平滑線性相位項(xiàng)的子光場(chǎng)，將半解析SPW算子概念推廣到平滑相位的通用形狀。在目標(biāo)平面上，所有傳播子光場(chǎng)被相干地相加，其中解析已知的平滑線性相位項(xiàng)以數(shù)值有效的方式使用第7節(jié)中介紹的逆拋物面分解技術(shù)（PDT）進(jìn)行處理。數(shù)值結(jié)果證明了新的傳播方法的有效性和準(zhǔn)確性。所有的模擬都是用光學(xué)軟件VirtualLab完成的。 TsGE cxIg  
z-b*D}&  
二.均勻介質(zhì)中的場(chǎng)追跡 qcN'e.A  
Q*b]_0Rb  
M6}3wM*4  
在光場(chǎng)追跡法中，光在線性、均勻和各向同性介質(zhì)中快速而精確的傳播是由諧波場(chǎng)的概念處理的。結(jié)果表明，任何電磁場(chǎng)都可以分解為一組諧波場(chǎng)[8,9]。在空間頻率域中，以特定角頻率ω0振蕩的單次諧波場(chǎng)定義為 'CN|'W)g7  
;W^o@*i{>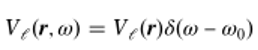  
(1) O
j^,m.R  
D`VM6/iQR  
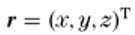
用位置向量和角頻率ω分別表示。請(qǐng)注意，下列理論是完全矢量的，因?yàn)樵谑剑?）中，諧波場(chǎng)分量代表三個(gè)電場(chǎng)分量和三個(gè)磁場(chǎng)分量，由于計(jì)算效率高，常用的諧波傳播技術(shù)基于FFT算法[10]。一種嚴(yán)格的傳播技術(shù)是SPW算子[5]，其中各諧波場(chǎng)分量的復(fù)振幅在與傳播方向正交的平面邊界上，通過傅里葉變換（FT）分解成一組平面波 VL*ovD%-  
)'4k|@8|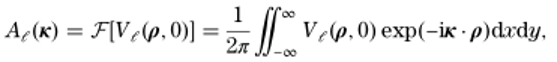  
(2) Mv6-|O  
TEaJG9RU>v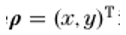  
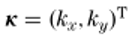
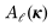
是初始平面邊界上的橫向位置向量，是對(duì)應(yīng)的空間頻率矢量。用表示的平面波通過與傳播因子相乘，在距離z上傳播 y8rm  
1+U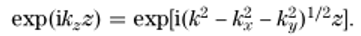  
(3) J52 o g4l  
:at$HCaK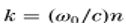  
表示折射率為n的均勻介質(zhì)中的波數(shù)，c為光的真空速度。最后，利用逆傅里葉變換將所有平面波疊加，從而得到SPW傳播算子， lHhUC16>  
.;*s`t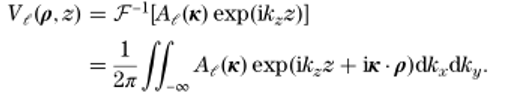  
(4) A$a1(8H  
(4Zts0O\  
從物理角度來看，SPW算子對(duì)任何傳播距離z和任何空間頻率矢量k[5]都是有效的。然而，對(duì)于長(zhǎng)的傳播距離，采樣公式（4）的數(shù)值工作量太大。對(duì)于非傍軸場(chǎng)，它包含高頻分量，數(shù)值工作量將變得更高。圖1示意性地示出了由于快速增長(zhǎng)的數(shù)值工作量而導(dǎo)致的SPW算子的有限范圍。 ZAXN6h  
一篇文獻(xiàn)中報(bào)道了兩個(gè)近似公式（4），以克服這一局限性。在這兩種情況下，即菲涅耳和遠(yuǎn)場(chǎng)積分，使用近似來分離球面相位項(xiàng)與積分的數(shù)值計(jì)算，并且球面相位項(xiàng)是被解析地處理的。這就大大減少了數(shù)值計(jì)算的工作量。然而，由于這些近似，兩種解決方案的適用性受到限制。菲涅耳積分[11]使用空間頻率分量的泰勒展開。用這種方法，將式（3）的球面相位函數(shù)替換為拋物線相位函數(shù)，從而得到式（4）中逆傅里葉變換積分的半解析解。如圖1所示，該概念僅適用于具有低空間頻率的傍軸場(chǎng)。對(duì)于長(zhǎng)傳播距離z，可以應(yīng)用遠(yuǎn)場(chǎng)積分[5]，其中公式（4）的逆傅里葉變換積分可以用固定相位的想法來半解析地求解。 !OuWPH. :  
>J>b>SU=-  
   =-}[^u1  
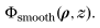
由于普通的自由空間傳播算子使用范圍的限制，先進(jìn)的傳播技術(shù)的發(fā)展對(duì)于非傍軸場(chǎng)追跡是必不可少的。這些技術(shù)應(yīng)覆蓋圖1中剩余的白參數(shù)空間，并在精度和數(shù)值計(jì)算之間取得最佳折衷。文獻(xiàn)[2,3,12-14]中有幾種方法。然而，這個(gè)問題的一般解決辦法仍不清楚。在實(shí)踐中，非傍軸諧波場(chǎng)振幅出現(xiàn)了采樣問題，其中部分包含強(qiáng)而光滑的相位項(xiàng)數(shù)學(xué)表達(dá)式為 nVI!
@qW