-
UID:317649
-
- 注冊時間2020-06-19
- 最后登錄2025-10-22
- 在線時間1881小時
-
-
訪問TA的空間加好友用道具

|
<\, �&�:<
文章來源:Bäuerle A, Bruneton A, Wester R, et al. Algorithm for irradiance tailoring using multiple freeform optical surfaces[J]. Optics express, 2012, 20(13): 14477-14485. M� �MAA�Ho
g�I)w^7G�i
主要內(nèi)容:本文基于最優(yōu)化質量傳遞(optimal mass transport)多自由曲面光學的設計算法,結合照明設計軟件FRED模擬了洗墻燈實例。使用該算法,可直接調整多面光學系統(tǒng)(在本文中,我們用了雙邊自由曲面)獲得了近似于預先確定照度分布,而同時可捕獲從光源發(fā)出的大部分光線。增加多曲面自由度可用來減小菲涅爾損失,包含加工上的約束以及減小零件尺寸。 #04{(G|~+E
Axel Bauerle, 1, 2 Adrien Bruneton, 1∗ Rolf Wester, 2 Q&u>7_, Du Jochen Stollenwerk, 1, 2 and Peter Loosen1, 2 99F>n��[5 1Chair for the Technology of Optical Systems, RWTH Aachen University, 52056 Aachen, M0O>Ljo4RN Germany �4)�c+t"h� 2Fraunhofer Institute for Laser Technology ILT, Steinbachstr. 15, 52074 Aachen, Germany C�xJfrI_�W i�Y0,WT}&n 摘要 �R'G'�&H{N
0�SJ�{@��* 自由曲面透鏡和反射鏡的設計能夠獲得非徑向對稱的照度分布,且同時保持光學系統(tǒng)的緊湊性。對于點狀光源來說,比如LED,為了增加發(fā)光效率往往需要捕獲一個寬角度的光源。這樣往往導致的結果是產(chǎn)生強彎曲光學元件,需要兩個透鏡面作用于總的光的折射,從而最小化菲涅爾損失。在本篇文章中,我們報道了一個基于最優(yōu)化質量傳遞(optimal mass transport)多自由曲面光學的設計算法,并結合光學工程仿真軟件FRED對一般照明問題給出了應用實例。 �_/|8%]��)
':,>eL#+uV 1.前言 �:~t<L%tYF
'Z\{D*�=V8 在照明應用中,透鏡和反射鏡可以以一種預先確定的方式上分配光線,市場上對這種透鏡及反射鏡的需求越來越多。為了獲得常用的光分布,光學設計中自由度數(shù)量必須高于傳統(tǒng)的光學元件,這就引入了自由曲面光學的概念,對此有眾多設計算法提出[1-5]。折射式光學元件(透鏡)在材料-空氣界面會遇到菲涅爾反射,控制其精準的路徑來避免損失難度較大。因為隨著光線角度傾斜菲涅爾反射在增加,因此理想情況是使用幾個自由曲面來增加系統(tǒng)的光學效率,在這種情況下,一個單透鏡面足以調整照度分布。 {�B@�*DQv�
�oz%h��)#; 到目前為止文獻中發(fā)布的設計算法,只有Minano、Benıtez[5]提出的SMS3D方法可以直接裁剪多平滑表面,且同時獲得預定的照度分布,甚至在一定程度上可把擴展光源考慮進去。然而,據(jù)作者所知,SMS3D算法只是在他們團隊內(nèi)部使用。對于點光源的情況,Ries 和Muschaweck[2]得出了一組偏微分方程來描述單個光學面,但一般對于多光學表面目前還沒有報道。 �B^X�y0fq�
{hxW�,mmA 在本文中,基于傳輸理論的公式[6],對兩個自由曲面和一個點光源發(fā)射器的照度調整問題,我們提出了靈活的近似解算法。此外,我們利用FRED軟件演示了對于一般照明設計任務的可行性。 �1 h<f�Jzh
�,q�8(]n�4 2.光線映射:有關光學設計的傳輸理論 ]|�,vCK�ju
�d�2ohW��| 在一般的公式中,質量傳輸理論講述了最優(yōu)路徑的計算,此計算允許從初始質量分布到目標質量分布的連續(xù)傳遞。就光學而言,光通量扮演了重要的角色,投射光源描述為在2維空間 上光通量密度 (圖1)。類似的,目標空間 上的光通量密度為 。為了清楚起見,在3維空間中,假定 平行于2維平面,光通量密度 和 在各自的局部笛卡爾坐標(x,y)下被參數(shù)化(圖1)。 XK1f�HfCEa 圖1.映射計算圖,點光源投射到平面 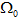 及目標照度投射到 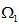 ,自由曲面位置在 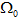 和 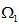 之間。 光學系統(tǒng)(自由曲面)的設計任務相當于發(fā)現(xiàn)一個微分同胚映射(光線映射),以便于照度分布轉換匹配目標分布: =f��o4x|{O 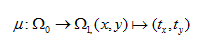 (1) 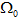 上的(x,y)在 上的(x,y)在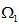 上的目標點。因為沿著無窮小燈管從光源到探測目標上光通量守恒,照度轉換公式可以寫為: +jc��df��} 上的目標點。因為沿著無窮小燈管從光源到探測目標上光通量守恒,照度轉換公式可以寫為: +jc��df��} 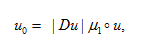 (2) 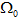 上積分此公式得到了總的能量守恒關系 上積分此公式得到了總的能量守恒關系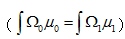 。
^��[en3aQ 。
^��[en3aQ
NeY"�6!;�k 因為映射u并不是獨一無二的[7],在光學設計任務中主要的限制是發(fā)現(xiàn)可引導光學表面連續(xù)可微的映射。這也就是所謂的表面法向矢量N可積條件[8] R @"`~�#$$
��>/�b^fAG N*curl(N)=0 (3)
LlU'��_}>
計算強制滿足方程(3)的光線映射并不是簡單的事情,因為由雅克比判決式(Monge-Ampere-type 方程)可知方程(2)一般等效于非線性二階偏微分方程。處理兩個光學表面而不是一個光學表面使這個問題更具挑戰(zhàn)性。 BApa^j\?�
N].4"0Jv-D 3.近似最優(yōu)化光線映射 e d_m +�NM
/a%*�u6�z@ 表面法線矢量場直接關系到映射信息(通過斯涅耳折射定律)。因此,即使現(xiàn)在還沒有被證實,看起來似乎是可信的:如果光線映射的旋度自身減小,表面法線矢量場的旋度可大幅度減小。 *0O<bm����
_~ �v-��:w 使用最新的質量傳遞理論有助于實現(xiàn)這一目標。在處理預定的目標函數(shù)這方面大部分的工作集中在尋找最佳映射。每個元件的位移、質量權重是具有代表性的二次函數(shù)。幾種不同的解決問題的方法已經(jīng)被提出[9]。本文中,我們關注于在圖像變換的背景下由Haker提出的一階、無參數(shù)方案[7]。 V{KjR�SVf=
-��eUV`&[4 點光源的光通量分布投射到方形的2維空間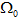 ,因此獲得了平坦的光通量密度μ。一個改進的立體投影通常用于獲得這個通量密度,與此同時控制可捕獲光錐角度。同樣的目標上的光通量分布投射到一個平行的方形區(qū)域 ,因此獲得了平坦的光通量密度μ。一個改進的立體投影通常用于獲得這個通量密度,與此同時控制可捕獲光錐角度。同樣的目標上的光通量分布投射到一個平行的方形區(qū)域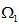 。如圖1所示。 7��7``��8, 。如圖1所示。 7��7``��8,
_O�$t��uC% Haker的步驟[7]是首先找到μ0和μ1初始映射關系(通常是在笛卡爾坐標軸上兩個連續(xù)1維數(shù)值積分),初始映射結果用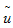 表示。 m+H%
大荔县|
浦城县|
满洲里市|
永州市|
咸阳市|
五大连池市|
蒙自县|
澎湖县|
信阳市|
桐柏县|
四子王旗|
屏东市|
清远市|
湟中县|
广丰县|
桃江县|
望城县|
南江县|
红安县|
慈溪市|
宿松县|
曲松县|
堆龙德庆县|
定州市|
洪江市|
崇义县|
郧西县|
瑞安市|
星子县|
大理市|
东丰县|
蒙阴县|
古田县|
孝感市|
慈溪市|
老河口市|
崇信县|
开封市|
莱芜市|
和林格尔县|
吉首市| 表示。 m+H%
大荔县|
浦城县|
满洲里市|
永州市|
咸阳市|
五大连池市|
蒙自县|
澎湖县|
信阳市|
桐柏县|
四子王旗|
屏东市|
清远市|
湟中县|
广丰县|
桃江县|
望城县|
南江县|
红安县|
慈溪市|
宿松县|
曲松县|
堆龙德庆县|
定州市|
洪江市|
崇义县|
郧西县|
瑞安市|
星子县|
大理市|
东丰县|
蒙阴县|
古田县|
孝感市|
慈溪市|
老河口市|
崇信县|
开封市|
莱芜市|
和林格尔县|
吉首市|
|