摘要 "�^[ '�y7i
�A � 'be�8 雙折射取向?qū)佑欣谝壕Ш械?span onclick="sendmsg('pw_ajax.php','action=relatetag&tagname=光學(xué)',this.id)" style="cursor:pointer;border-bottom: 1px solid #FA891B;" id="rlt_2">光學(xué)性能,這對(duì)測(cè)量方位角錨定能量的光學(xué)方法也有意義。 我們得到了計(jì)算受取向?qū)舆t滯影響的液晶扭曲角的修正值的分析方程. 獲得了AtA-2和AtA-0042偶氮染料光取向
材料的方位角錨定能量測(cè)量數(shù)據(jù): >10-4J/m2,在廣泛的曝光劑量0.04 -5.12 J/cm2范圍內(nèi).
"�Y.tht� H 2|y"!�JqE1
關(guān)鍵詞 I|�!OY`ko 方位錨定能;液晶取向;延遲;光配向 XX!%RE�`M8
�G��Vr1`l� 介紹 \7eUw,~Q>� 對(duì)方位角錨定能量的探索是液晶盒制造工藝優(yōu)化和新材料研究的一個(gè)有用方式。 標(biāo)準(zhǔn)的光學(xué)方法[1]被廣泛用于測(cè)定各種取向材料的方位角錨定能量。按照該方法,線偏振光波長(zhǎng)λ--全波的旋轉(zhuǎn)僅由扭曲向列型液晶(LC)盒的扭曲角φ0決定;并測(cè)量波長(zhǎng)λ處光通過LC盒傳播時(shí)的偏振面旋轉(zhuǎn)角γ。 "��c�Gk)�s 在取向?qū)拥碾p折射可以忽略不計(jì)的情況下,偏振面旋轉(zhuǎn)的角度γ等于液晶盒內(nèi)的實(shí)際扭曲角φ,那么我們可以簡(jiǎn)單地假設(shè)公式1: 7WqH�&vU| VCfl`A�q'l 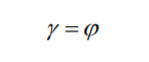
(1)
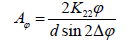
(2)
�?�81c �4w 可是對(duì)于光配向材料的情況下, 特別是在偏振光照射下發(fā)生分子定向的偶氮染料 [2,3], 取向?qū)拥墓庵码p折射是很重要的,它對(duì)于光在LC盒中傳播時(shí)的偏振平面旋轉(zhuǎn)角度也有貢獻(xiàn)。 ]c*�4J\s��
F�Uz�zB94a 所以取向?qū)拥碾p折射需要被考慮在內(nèi)。 Jr4�Ky<G_i
P;
黎川县|
饶阳县|
广昌县|
宣武区|
汨罗市|
洛浦县|
大石桥市|
织金县|
安义县|
全州县|
渭南市|
沁水县|
西峡县|
岳阳县|
岑溪市|
阜平县|
东辽县|
沛县|
安西县|
华安县|
板桥市|
昭觉县|
肥城市|
肥西县|
乌鲁木齐县|
棋牌|
白河县|
同江市|
崇阳县|
金川县|
德保县|
寻甸|
河东区|
穆棱市|
莱州市|
高安市|
昌黎县|
黑龙江省|
中西区|
德清县|
元谋县|