| infotek | 2020-12-23 09:38 |
基于多自由曲面的照度調(diào)整算法文章來(lái)源:Bäuerle A, Bruneton A, Wester R, et al. Algorithm for irradiance tailoring using multiple freeform optical surfaces[J]. Optics express, 2012, 20(13): 14477-14485. 主要內(nèi)容:本文基于最優(yōu)化質(zhì)量傳遞(optimal mass transport)多自由曲面光學(xué)的設(shè)計(jì)算法,結(jié)合照明設(shè)計(jì)軟件FRED模擬了洗墻燈實(shí)例。使用該算法,可直接調(diào)整多面光學(xué)系統(tǒng)(在本文中,我們用了雙邊自由曲面)獲得了近似于預(yù)先確定照度分布,而同時(shí)可捕獲從光源發(fā)出的大部分光線。增加多曲面自由度可用來(lái)減小菲涅爾損失,包含加工上的約束以及減小零件尺寸。 Axel Bauerle, 1, 2 Adrien Bruneton, 1∗ Rolf Wester, 2 Jochen Stollenwerk, 1, 2 and Peter Loosen1, 2 1Chair for the Technology of Optical Systems, RWTH Aachen University, 52056 Aachen, Germany 2Fraunhofer Institute for Laser Technology ILT, Steinbachstr. 15, 52074 Aachen, Germany 摘要 自由曲面透鏡和反射鏡的設(shè)計(jì)能夠獲得非徑向?qū)ΨQ(chēng)的照度分布,且同時(shí)保持光學(xué)系統(tǒng)的緊湊性。對(duì)于點(diǎn)狀光源來(lái)說(shuō),比如LED,為了增加發(fā)光效率往往需要捕獲一個(gè)寬角度的光源。這樣往往導(dǎo)致的結(jié)果是產(chǎn)生強(qiáng)彎曲光學(xué)元件,需要兩個(gè)透鏡面作用于總的光的折射,從而最小化菲涅爾損失。在本篇文章中,我們報(bào)道了一個(gè)基于最優(yōu)化質(zhì)量傳遞(optimal mass transport)多自由曲面光學(xué)的設(shè)計(jì)算法,并結(jié)合光學(xué)工程仿真軟件FRED對(duì)一般照明問(wèn)題給出了應(yīng)用實(shí)例。 1.前言 在照明應(yīng)用中,透鏡和反射鏡可以以一種預(yù)先確定的方式上分配光線,市場(chǎng)上對(duì)這種透鏡及反射鏡的需求越來(lái)越多。為了獲得常用的光分布,光學(xué)設(shè)計(jì)中自由度數(shù)量必須高于傳統(tǒng)的光學(xué)元件,這就引入了自由曲面光學(xué)的概念,對(duì)此有眾多設(shè)計(jì)算法提出[1-5]。折射式光學(xué)元件(透鏡)在材料-空氣界面會(huì)遇到菲涅爾反射,控制其精準(zhǔn)的路徑來(lái)避免損失難度較大。因?yàn)殡S著光線角度傾斜菲涅爾反射在增加,因此理想情況是使用幾個(gè)自由曲面來(lái)增加系統(tǒng)的光學(xué)效率,在這種情況下,一個(gè)單透鏡面足以調(diào)整照度分布。 到目前為止文獻(xiàn)中發(fā)布的設(shè)計(jì)算法,只有Minano、Benıtez[5]提出的SMS3D方法可以直接裁剪多平滑表面,且同時(shí)獲得預(yù)定的照度分布,甚至在一定程度上可把擴(kuò)展光源考慮進(jìn)去。然而,據(jù)作者所知,SMS3D算法只是在他們團(tuán)隊(duì)內(nèi)部使用。對(duì)于點(diǎn)光源的情況,Ries 和Muschaweck[2]得出了一組偏微分方程來(lái)描述單個(gè)光學(xué)面,但一般對(duì)于多光學(xué)表面目前還沒(méi)有報(bào)道。 在本文中,基于傳輸理論的公式[6],對(duì)兩個(gè)自由曲面和一個(gè)點(diǎn)光源發(fā)射器的照度調(diào)整問(wèn)題,我們提出了靈活的近似解算法。此外,我們利用FRED軟件演示了對(duì)于一般照明設(shè)計(jì)任務(wù)的可行性。 2.光線映射:有關(guān)光學(xué)設(shè)計(jì)的傳輸理論 在一般的公式中,質(zhì)量傳輸理論講述了最優(yōu)路徑的計(jì)算,此計(jì)算允許從初始質(zhì)量分布到目標(biāo)質(zhì)量分布的連續(xù)傳遞。就光學(xué)而言,光通量扮演了重要的角色,投射光源描述為在2維空間 上光通量密度 (圖1)。類(lèi)似的,目標(biāo)空間 上的光通量密度為 。為了清楚起見(jiàn),在3維空間中,假定 平行于2維平面,光通量密度 和 在各自的局部笛卡爾坐標(biāo)(x,y)下被參數(shù)化(圖1)。 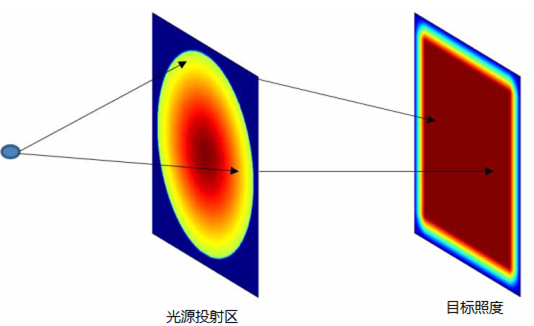 圖1.映射計(jì)算圖,點(diǎn)光源投射到平面 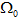 及目標(biāo)照度投射到 及目標(biāo)照度投射到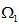 ,自由曲面位置在 ,自由曲面位置在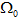 和 和 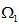 之間。 之間。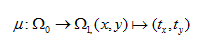 (1) (1)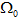 上的(x,y)在 上的(x,y)在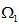 上的目標(biāo)點(diǎn)。因?yàn)檠刂鵁o(wú)窮小燈管從光源到探測(cè)目標(biāo)上光通量守恒,照度轉(zhuǎn)換公式可以寫(xiě)為: 上的目標(biāo)點(diǎn)。因?yàn)檠刂鵁o(wú)窮小燈管從光源到探測(cè)目標(biāo)上光通量守恒,照度轉(zhuǎn)換公式可以寫(xiě)為: 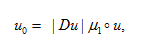 (2) (2)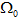 上積分此公式得到了總的能量守恒關(guān)系 上積分此公式得到了總的能量守恒關(guān)系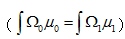 。 。 因?yàn)橛成鋟并不是獨(dú)一無(wú)二的[7],在光學(xué)設(shè)計(jì)任務(wù)中主要的限制是發(fā)現(xiàn)可引導(dǎo)光學(xué)表面連續(xù)可微的映射。這也就是所謂的表面法向矢量N可積條件[8] N*curl(N)=0 (3) 計(jì)算強(qiáng)制滿足方程(3)的光線映射并不是簡(jiǎn)單的事情,因?yàn)橛裳趴吮扰袥Q式(Monge-Ampere-type 方程)可知方程(2)一般等效于非線性二階偏微分方程。處理兩個(gè)光學(xué)表面而不是一個(gè)光學(xué)表面使這個(gè)問(wèn)題更具挑戰(zhàn)性。 3.近似最優(yōu)化光線映射 表面法線矢量場(chǎng)直接關(guān)系到映射信息(通過(guò)斯涅耳折射定律)。因此,即使現(xiàn)在還沒(méi)有被證實(shí),看起來(lái)似乎是可信的:如果光線映射的旋度自身減小,表面法線矢量場(chǎng)的旋度可大幅度減小。 使用最新的質(zhì)量傳遞理論有助于實(shí)現(xiàn)這一目標(biāo)。在處理預(yù)定的目標(biāo)函數(shù)這方面大部分的工作集中在尋找最佳映射。每個(gè)元件的位移、質(zhì)量權(quán)重是具有代表性的二次函數(shù)。幾種不同的解決問(wèn)題的方法已經(jīng)被提出[9]。本文中,我們關(guān)注于在圖像變換的背景下由Haker提出的一階、無(wú)參數(shù)方案[7]。 點(diǎn)光源的光通量分布投射到方形的2維空間 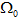 ,因此獲得了平坦的光通量密度μ。一個(gè)改進(jìn)的立體投影通常用于獲得這個(gè)通量密度,與此同時(shí)控制可捕獲光錐角度。同樣的目標(biāo)上的光通量分布投射到一個(gè)平行的方形區(qū)域 ,因此獲得了平坦的光通量密度μ。一個(gè)改進(jìn)的立體投影通常用于獲得這個(gè)通量密度,與此同時(shí)控制可捕獲光錐角度。同樣的目標(biāo)上的光通量分布投射到一個(gè)平行的方形區(qū)域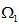 。如圖1所示。 。如圖1所示。 | |