| summer20200907 | 2021-02-22 11:33 |
Macleod中的偏振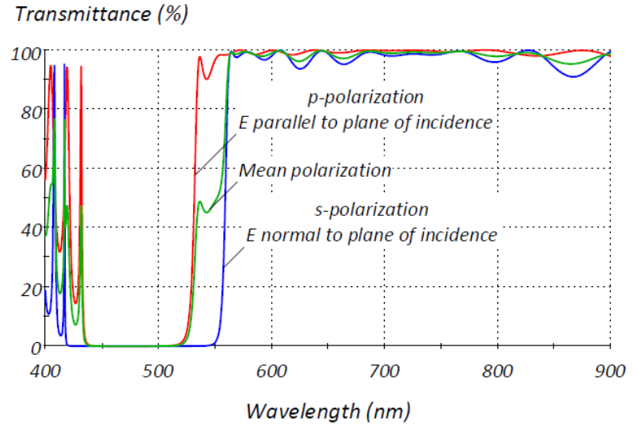 圖1. 在45°條件下計算的600nm長波通濾光片,顯示了P偏振、S偏振和平均偏振的透射率。 讓我們將討論局限于完全各向同性的材料。所涉及的過程是線性的,允許我們將任何問題分解為一系列可以單獨遵循的簡單分量。對于Essential Macleod中的所有計算,基本分量是線偏振平面波(或單色光)。 當(dāng)我們討論偏振時,我們經(jīng)常提到線偏振或平面偏振、圓偏振和橢圓偏振。在計算中,所有這些偏振被表示為兩個正交線偏振的組合,其可以單獨計算并且在透射或反射中的取向不變。它們有時被稱為偏振的本征模式,這在斜入射時尤為重要。光學(xué)薄膜的作用是改變每種組分的振幅和相位。膜層的性能量化了這些變化。 | |