| infotek | 2025-01-10 07:57 |
JCMsuite應(yīng)用:散射體的光學(xué)手性響應(yīng)在電磁能量的情況下,消光由散射和損失[2]組成。對應(yīng)的手性參量是光學(xué)手性的消光 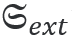 散射 散射 ,以及體積 ,以及體積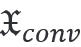 和界面上 和界面上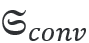 的手性轉(zhuǎn)換。這就得到了守恒定律 的手性轉(zhuǎn)換。這就得到了守恒定律 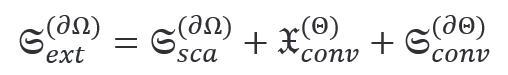 積分是在散射體的外表面∂Ω和體積Θ以及表面∂Θ上進(jìn)行的。 這些參量在JCMsuite中命名,如下表所示。更多細(xì)節(jié)可以在這里找到。 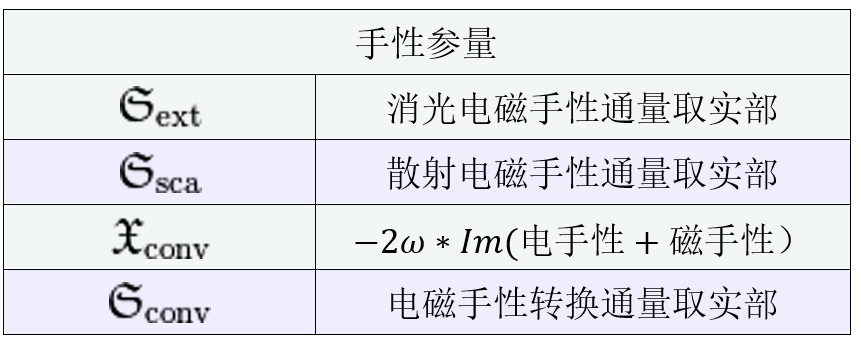 作為案例展示,我們計(jì)算散射體的手性響應(yīng)如下圖所示: 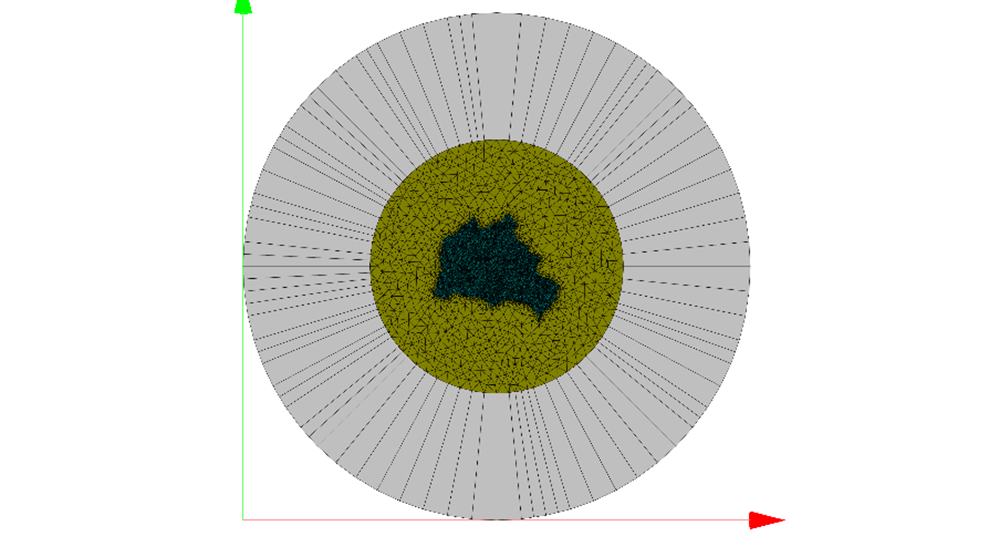 它的直徑是一個(gè)波長的量級,它的介電常數(shù)固定為ε=4.5。在下面,我們將改變散射體的磁導(dǎo)率μ,并觀察預(yù)測的對偶對稱性[3]對于恒定比率ε/μ的散射體及其環(huán)境。周圍的材料是ε=μ=1的空氣。 由于散射體是無損的和各向同性的,在它的體積內(nèi)將沒有轉(zhuǎn)換。請參考四分之一波片的案例,以獲得更多關(guān)于體積轉(zhuǎn)換的信息。 在這里,所需的參量被計(jì)算為如上所述的電磁手性通量的通量積分。如下圖所示,對于接近對偶對稱的材料,轉(zhuǎn)換趨向于零。 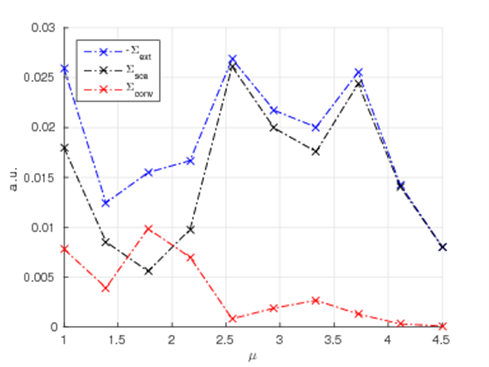 在固定介電常數(shù)ε=4.5下,散射體的磁導(dǎo)率μ的變化。 該散射體是對偶的ε/μ=1,產(chǎn)生零手性轉(zhuǎn)換。 在JCMsuite中,所有手性密度都是相似的。例如,我們在下面的圖中展示了增強(qiáng)的近場光學(xué)手性密度的電子部分。這是一個(gè)后處理過程,即ExportFields:輸出參量電手性密度。 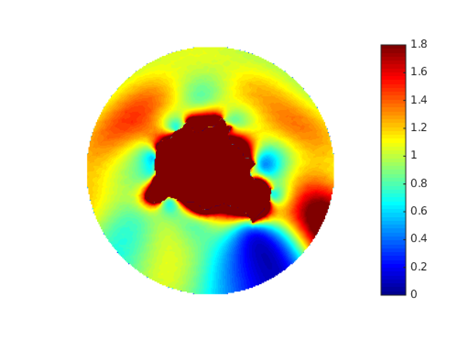 具有ε/μ=1的雙散射體的光手性密度X的近場增強(qiáng) 參考文獻(xiàn) [1] Philipp Gutsche, Lisa V. Poulikakos, Martin Hammerschmidt, Sven Burger, and Frank Schmidt. Time-harmonic optical chirality in inhomogeneous space. In SPIE OPTO, Vol.9756m pages 97560X. International Society for Optics and Photonics, 2016. [2] Craig F. Bohren and Donald R. Huffman. Absorption and Scattering of Light by Small Particles. John Wiley & Sons, 1940. [3] Ivan Fernandez-Corbaton. Helicity and duality symmetry in light matter interactions: Theory and applications. PhD thesis, Macquarie University, Department of Physics and Astronomy, 2014. |
|